This tutorial explains how to calculate probability of a range using Z score (standard normal random variable).
You may also want to read:
Excel Range, Variance, Standard Deviation
Calculate Z Score and probability using SPSS and Excel
Calculate probability of a range using Z Score
Assume that a random variable is a normally distributed (a normal curve), given that we have the standard deviation and mean, we can find the probability that a certain value range would occur.
I will demonstrate the this concept using an example.
Question
A fund has a return with a mean of 10% and standard deviation of 5%. What is the probability of losing money?
Answer
Losing money means the return < 0%. When calculating probability, we represent this statement as
P (X < 0)
Step 1 – Calculate Z Score
The first step is to standardize the target variable value into a standard normal random variable (Z Score) using the known standard deviation and mean. Z Score is an indicator of how far the value is away from the mean.
Formula:
Z score = (X-μ)/σ
= (target value - population mean) / population standard deviation
= (0 - 10)/5
= -2 (2 standard deviation below mean)
Meaning of the Z score result:
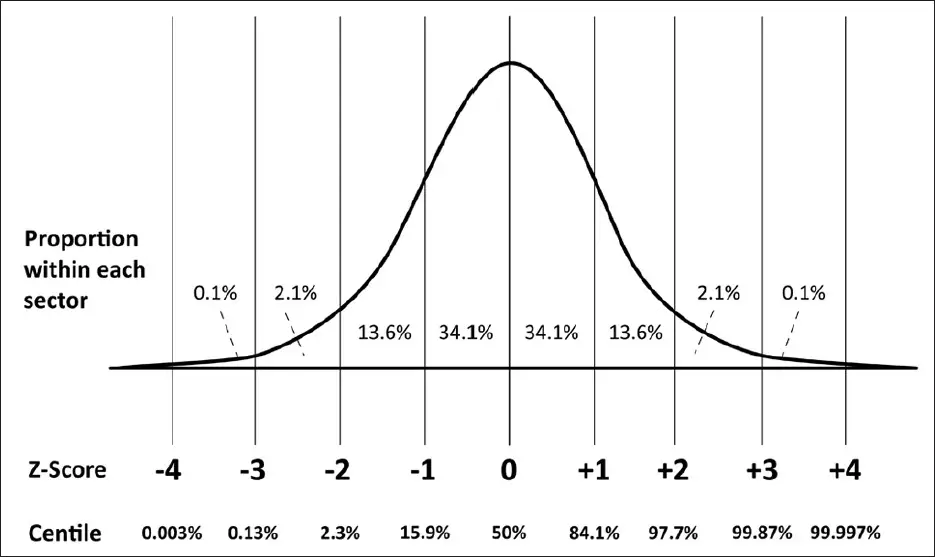
Z score is a standardized standard deviation (no matter what the actual standard deviation is, it is standardized from -4 to 4), and therefore we can calculate the investment return and probability. You can image each Z value corresponds to a standard deviation, probability and investment return value.
Z score = 0 : variable value = mean (10% investment return)
Z score > 0 : variable value > mean, Z score = 1 means 1 standard deviation above the mean, 2 = 2 standard deviation
Z score < 0 : variable value < mean
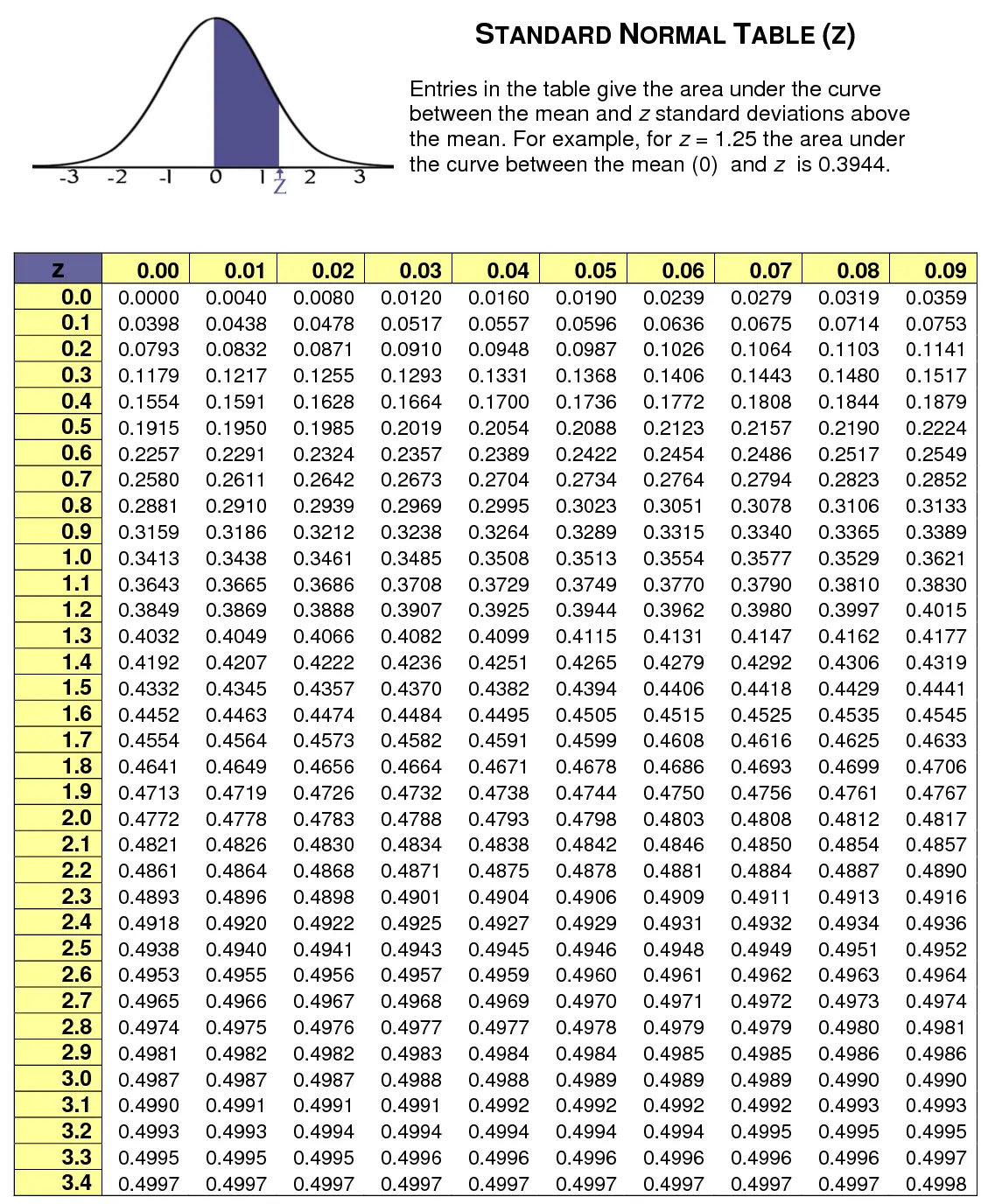
Step 2 – Look up probability from Standard Normal Table
The value in the first column (0.00, 0.01, 0.02…) is the first decimal place of Z, the value in the first row (0.00, 0.01, 0.02…) is the second decimal place of Z.
For example, the calculated Z value is 0.13, then we look for the 0.10 in the first column, and look for 0.03 in the first row, the result is 0.0517.
Standard Normal Table only provides positive Z value but not negative Z value, it is because the normal curve is a regular bell shape, it makes no difference between positive Z and negative Z. To save space, it is no point to repeat the whole table again with a negative Z value. In other words, the table only shows probability of half the curve, therefore the maximum probability you can find is 0.4998 (ideally it should be 0.5).
In our example, since the the probability of +2 and -2 are the same under the normal curve, we can simply look for Z = 2.00, the result is 0.4772.
Step 3 – Interpreting the result
As spoken above, the probability we looked at is half the normal curve from the middle point. Result 0.4772 is referring to the probability from Z = 0 (the mean of 10% return) to Z= -2 (0% return), but since we want the probability of <0% return return (Z < -2), we need to subtract 0.4772 from 0.5 (probability of half the normal curve area).
To represent this concept in formula,
P (X < 0)
= P (Z < -2)
= 0.5 – 0.4772
=0.0228
According to the formula
Z score = (X-μ)/σ
= (target value - mean) / standard deviation
Increasing the standard deviation will decrease Z score, lower Z score means lower probability, thus increasing chance of losing money.
What’s Next?
Calculating Z Score manually and finding the probability in Standard Normal Table is only for you to learn the concept, you can get the value quickly using SPSS and Excel.
You should also read the below article:
Calculate Z Score and probability using SPSS and Excel