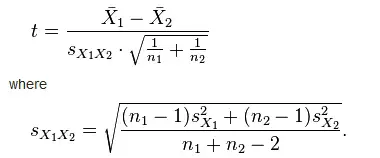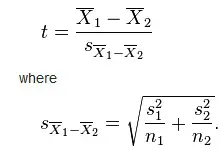This SPSS Excel tutorial explains how to perform one tailed and two tailed Independent T Test in Excel and SPSS.
What is Independent T Test
In statistical inference, we are interested to know whether a small sample comes from a population. To inference using sample mean, when the population standard deviation and population mean are known, we can use Z test to interference the population mean from sample mean.
In reality, we do not have data of the whole population. Without the population standard deviation, we use T Test (also known as Student’s t Test) to interference the population mean from sample mean.
There are basically three kinds of T Test in statistics:
| One sample T Test | Test whether a target mean value is equal to the population mean |
| Independent T Test | Test whether the population mean from two individual samples are equal. For two samples, you can also use One Way ANOVA, but ANOVA is not directional. |
| Paired-samples T Test | Test whether the population mean between paired observations are equal |
Independent sample T Test can have to types: equal population variance and unequal population variance.
For equal population variance:
For unequal population variance:
In Excel, you can use F-Test Two-Sample for Variances to test the probability of equal variance before you select the appropriate T Test.
In SPSS, when you generate the test result for Independent-Samples T Test, F value will be generated under the section Levene’s Test.
Independent T Test – using Excel
Suppose we try to find if Finance graduates have a higher salary than computer science graduates.
We make the below hypothesis
Ho: mean of finance graduate salary - mean of CS graduate salary = 0 H1: mean of finance graduate salary - mean of CS graduate salary > 0
Because our H1 is directional, the test is 1-tailed.
Before doing T test in Excel, make sure you have enabled Data Analysis Add-In.
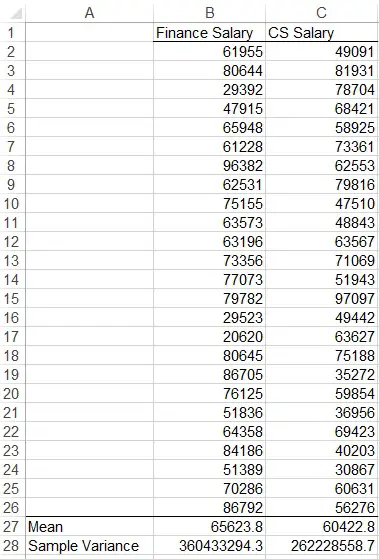
Step 1: Calculate sample variance
Prepare a data source as below, and then calculate the sample variance using VAR.S Function.
Step 2: Test variance is equal or unequal
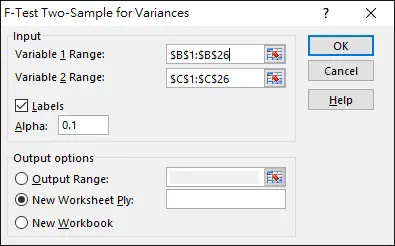
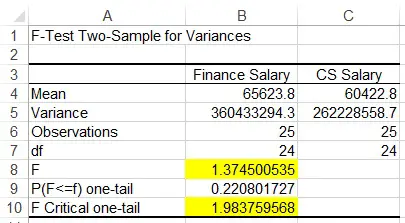
Navigate to Data > Data Analysis > F-Test Two-Sample for Variances
Fill in the Variable 1 and 2 Range. Note that for Variable 1 Range, you have to fill in the larger variance one, that’s why we have to calculate the sample variable previously.
Now a table is generated. The null hypothesis is the variance is equal, at confidence level 95%, F value is 1.9837, now the calculated F value is only 1.37, therefore we do not have enough evidence to reject H0, meaning the variance is equal.
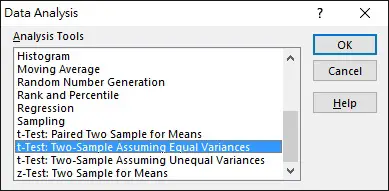
Step 3: Two-Sample Assuming Equal Variances
Since we have tested that the variance is equal, now we select Data analysis t-Test:Two-Sample Assuming Equal Variances. Otherwise, select t-Test: Two-Sample Assuming Unequal Variances.
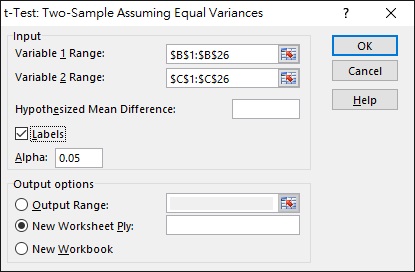
Navigate to Data > Data Analysis > t-Test: Two-Sample Assuming Equal Variances
Again, select the higher sample variance range for Variable 1 Range.
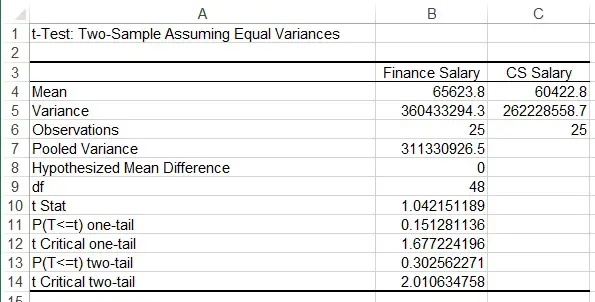
Since t Stat (1.042) is less than t Critical one-tail (1.677), Ho is not rejected, meaning salary of finance graduate and cs graduate have no difference.
You can also use Excel T.Test Function to directly get the P value.
Independent T Test – using SPSS
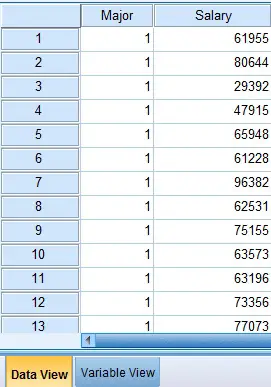
Prepare your data source as below format. 1 is Finance, 2 is CS.
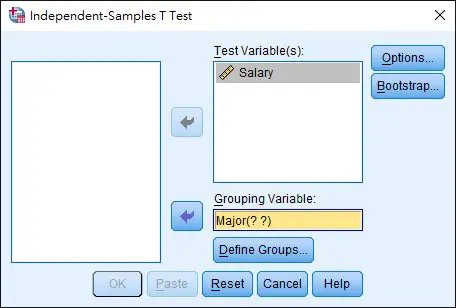
In the menu, navigate to Analyze > Compare Means > Indepent-Samples T Test
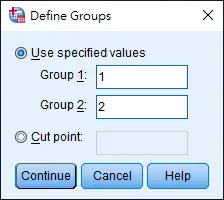
Select the variables as below, then click on Define Groups
We have to define Group 1 as 1 (Finance), Group 2 as 2 (CS). SPSS calculates the T statistics using Group 1 mean – Group 2 mean. If we want positive T statistics, Group 1 mean has to be larger than Group 2.
According to IBM website:
SPSS has no specific procedure or dialog box to run a one-tailed test for differences of means. The procedure for the one-tailed test is the same as for the two-tailed test. There are two issues here, though. First is to have an idea of which direction you want the t-statistic to go. If you expect that group 1 has a higher mean than group 2, you will be looking for a positive t-statistic (since SPSS will use the mean of group 1 minus the mean of group 2 as the numerator in computing the t statistic). Make sure that you know which direction the t statistic is going and what that direction indicates.
The significance for this test is the displayed significance divided by two. Since the t statistic has a symmetrical distribution, the “significant” tails will have the same probability (e.g. in a two-tailed test, a .05 criteria reflects that the .025 tails will reflect significance). Since we are looking at only one of those tails, we would divide the significance in half to determine if the t statistic is significant or not
Click on Continue > OK to generate the result
There are two parts of testing in the Independent Samples Test table.
On the left hand side is the Levene’s Test, Ho assumes two variances are equal. Since the significance level >0.05, we do not reject Ho, meaning the variances are equal.
On the right hand side of the Independent Samples Test table, it shows both results for equal variances and unequal variances. Based on the Levene’s Test on the left, we only read the data on the top row (equal variances).
Finally since we are testing one tailed, we divide the two tailed probability by 2, then we have P value 0.151. Since P > 0.05, we do not reject Ho, meaning salary of finance graduate and cs graduate have no difference.